Mathematics

Intent

The intent of the Saint Edmund’s mathematics curriculum is to develop independent and competent mathematicians who are able to apply their skills in any occupation or activity they choose later in life. We aim to create a confidence with numeracy and an ability to make reasoned financial decisions and strive to demonstrate the inherent joy in tackling challenging problems and finding a satisfying solution.

Our curriculum is designed to meet the aims of the national curriculum and help learners:

• become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
• reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language
• solve problems by applying their mathematics to a variety of routine and nonroutine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

Implementation

The curriculum is planned and contributed too by all specialist maths teachers in the department. Lessons follow a consistent and successful model based around the principles of Learning Cycle and contain opportunities for adapted teaching strategies throughout. Series of lessons will be linked together into units and progress will be reflected on and checked against Wilfs throughout. All lessons follow an “I do, we do, you do” structure, with every modelled example followed by a mini-whiteboard activity to check understanding and then independent practice to embed/extend the learning.

Year 7, 8 and 9 follow a spiral style curriculum, starting with the fundamentals before moving to more advanced content, always linked to the appropriate level of ability for the learner. Each term’s curriculum contains catch-up/extension opportunities to give teacher’s flexibility to spend more time delivering a topic if necessary or extend the learning further.

As a department we are interested in the forgetting curve and the research surrounding it, implementing strategies to reduce the deterioration of hard-won knowledge where possible using spaced recall. To this end every lesson begins with a starter challenging recall of the preceding lesson, end of unit assessments force recall of recently taught material, problem solving sessions encourage recall and application of several skills taught over the last month and termly assessments bring recall of the previous 3 months of learning together. Interspersed within these will be homework tasks on the more prominent skills, completed using an electronic platform, where St Edmund’s is the top 1% of schools for providing feedback to students.

We are a reflective department and organically adapt our delivery overtime; the KS4 and KS3 curriculums are regularly reviewed and lessons/curriculum time adapted based upon pupil performance as we push to maximise the progress of all our learners.

Outcome

Below are the results for the Mathematics GCSE from the last 4 academic years, each year our cohorts perform above the national average.

However, the results we are most proud of as a department are our progress scores, these show on average how much more progress was made within our school compared to other similar students nationally. A score of 0.5 would mean students did half a grade better with us than students across the country.

*2021 and 2020 we based of centre assessed grades.

Key Stage 3 (Year 7 - 9)

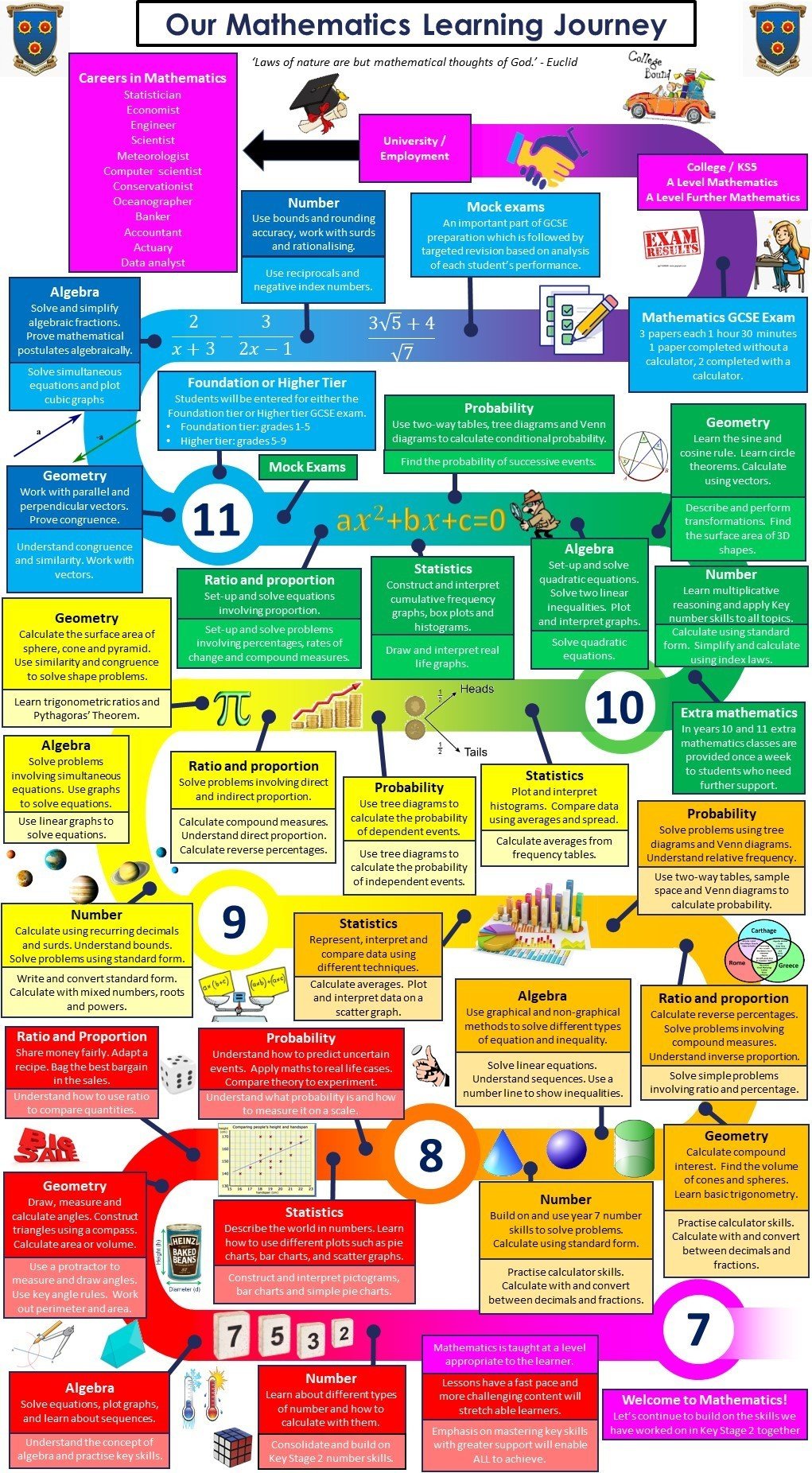
The Saint Edmund’s KS3 curriculum builds upon the excellent teaching and progress students receive from our primary feeder schools. It aims to push the students to achieve above traditional expectations, moving learners who are broadly in line with the age related expectations to learners who are above age related expectations. We ensure that the entire K3 curriculum is delivered at the appropriate level for each learner. You can see the scheme of work which we follow in the KS3 Curriculum Map.

Year 7 Summer Term -  

In the first half of this term, pupils will be continuing to learn about constructions as well as learning about ratio and proportion, angles and transformations. 

Within constructions, students will be learning how to use their compass to perform a variety of constructions such as triangles and some will also learn how to construct bisectors. They will also learn how to write and simplify a ratio, as well as how quantities can be shared in a given ratio. As part of this unit, they will also learn how to scale recipes and determine what the best purchase might be based on differing quantities and prices. 

In the angle unit, students will learn what the different basic angle facts are and how to find angles in parallel lines. Some students will also learn about angles in polygons and all about congruence and similarity. Throughout this topic students will also learn how to answer angle questions that involve algebra. Pupils will also learn about the four different transformations – reflections, rotations, translations and enlargements – and how to both perform and describe each one.  

In the second half of the summer term, students will learn about the final topic of displaying data. Each class will then have the opportunity to consolidate what they have learnt as well as extend their knowledge further in preparation for Year 8. 

In this final unit, pupils will look at how data is collected and how it can be displayed in a variety of formats such as bar charts, pie charts, two-way tables and scatter diagrams. Some students will also look at conversion graphs and distance-time graphs as well as have the opportunity to perform their own investigation. Each class will then follow an individualised scheme of work based on their own needs for consolidation and extension. At this time, please contact the teacher if you need more information on what is being covered.   

With all the topics the pupils will be applying their knowledge to problem-solving, applying it to real-life scenarios and cross-curricular topics. " 

Year 8 Summer Term - 

The first half of this term pupils build upon the Year 7 summer term topics of ratio and proportion, angles and transformations. They will consolidate Year 7 skills and then build on these to be able to work with direct proportion and density, mass and volume. Some students will also build on this further to learn about 3-part ratios and speed, distance and time. 

After consolidating what they have learnt about angles in Year 7, with all pupils now learning about angles in polygons, some pupils will have a much deeper focus on problem-solving and more in-depth questions. When learning about transformations, all pupils will revisit the four previously learnt transformations, with some learning about enlargements involving fractional and/or negative scale factors. 

In the second half of this term, pupils build upon the Year 7 spring term topic of displaying data, as well as having the opportunity to catch up on work missed or extend their knowledge in preparation for beginning the GCSE Scheme of Work in Year 9. 

Pupils will review the skills learnt in Year 7, with all pupils now learning about conversion graphs and distance-time graphs and some pupils will learn about these, pie charts and scatter graphs in more depth. Each class will then follow an individualised scheme of work based on their own needs for consolidation and extension. At this time, please contact the teacher if you need more information on what is being covered. 

With all the topics the pupils will be applying their knowledge to problem-solving, applying it to real-life scenarios and cross curricular topics." 

"

Key Stage 4 (Year 10 - 11)

Exam board: Edexcel    

Specification: 1MA1

Tiers of entry: Higher and Foundation

Exam: 3 papers, each 33.3% of total grade. 1 paper completed without a calculator, 2 completed with a calculator.

All the content within the specification is covered to the appropriate level of the students, whether they are Foundation or Higher tier students. Typically, the final half-terms of Year 11 are spent using high quality exam preparation resources and supporting revision.

The overview of topics taught, beginning in Year 9, can be found below:

Foundation:

 Higher

Extra-curricular Activities

Practical Lessons

The Mathematics department at Saint Edmund's includes practical uses of Mathematics when appropriate, some examples are below.

Students in Year 9 studying right-angled triangles spend one of their lessons outside of the classroom learning how to use trigonometry to determine the height of a variety of school buildings and some local buildings.

Taking inspiration from Ezekiel 4:9, a group of students in Year 8 learnt one of the many cross-curricular links in maths. In their first lesson, students learnt to scale a recipe for "Ezekiel Muffins" up and down and how they would scale it for their own needs. In the following lesson, students made use of the iPad to work out where they should purchase the ingredients to ensure they got them for the best value. For the final lesson, students used the food technology room to bake their own Ezekiel muffins, adding their own additional toppings and flavours. 

Homework

Sparx - St Edmund's Catholic School (sparxmaths.uk)

In Maths, homework is set every week on a Tuesday at 8am and is due the following Monday at 8am. The expectation is for Years 7 - 10 to spend approximately 30 minutes actively working on the homework each week, whilst those in Year 11 spend approximately 60 minutes actively working on the homework each week to help prepare them for their exams.

Useful links:

Website for our exam board, Edexcel, which contains a link to the Mathematics GCSE specification we follow:

https://qualifications.pearson.com/en/qualifications/edexcel-gcses/mathematics-2015.html

Mr Barton Maths - Videos and GCSE exam-style questions - GCSE Maths Takeaway Revision on Mr Barton Maths

Corbett Maths - Videos, worksheets and GCSE exam-style questions - Videos and Worksheets – Corbettmaths

Maths Genie - Videos and GCSE exam-style questions - Maths Genie • Learn GCSE Maths for Free

Resources

Students are expected to supply their own calculator and should purchase one before starting at Saint Edmund’s Catholic School. We provide books, homework and all additional resources necessary for the successfully achievement of the learners in our charge.

Recommended reading

In addition to the books listed on the reading canon for KS3, we also recommend the following books:

For improving readers:

Sir Cumference and the Dragon of Pi – Cindy Neuschwander and Wayne Geehan

Sir Cumference and the Dragon of Pi is a fun way to learn about math! With its colourful pictures and exciting story, the book makes math really interesting. You'll get to join Sir Cumference on his adventures and learn all about pi and shapes. It's a book that makes learning math super fun!

Year 10